6. Normal Distribution & Continuous Random Variables
Standard Normal Distribution
Struggling with Statistics for Business?
Join thousands of students who trust us to help them ace their exams!Watch the first videoMultiple Choice
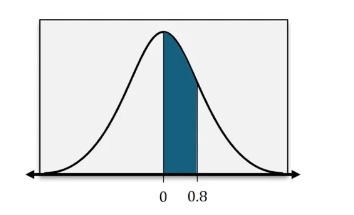
Find the area of the shaded region under the standard normal distribution.
A
0.7881
B
0.7119
C
0.2119
D
0.2881
Verified step by step guidance1
Understand that the shaded region under the standard normal distribution curve represents the probability between two z-scores. In this case, the z-scores are 0 and 0.8.
Recall that the standard normal distribution is symmetric around the mean, which is 0, and has a standard deviation of 1. The total area under the curve is 1.
Use the standard normal distribution table (z-table) to find the cumulative probability for z = 0.8. This value represents the area under the curve from the far left up to z = 0.8.
Find the cumulative probability for z = 0 using the z-table. This value represents the area under the curve from the far left up to z = 0.
Subtract the cumulative probability at z = 0 from the cumulative probability at z = 0.8 to find the area of the shaded region between these two z-scores.
9:47mWatch next
Master Finding Standard Normal Probabilities using z-Table with a bite sized video explanation from Patrick
Start learning
